You don't get to be an Engineer or a Product Designer without a fundamental understanding of Maths. Take a look at how the world's most recognisable symbol is used on an everyday basis to make our clients' products become a reality.
At Raymont-Osman, we're good with numbers! Either through manual hand calculations, or through our extensive suite of test and simulation tools. Maths forms an integral part of the design process. We pride ourselves in supporting our clients throughout the product life cycle, including: initial concept design and subsequent development, physical design, precision testing and simulation, product and process analysis and ongoing manufacturing support.
Put simply - our products are made to function in the real world. But before we get there, our team need to ensure that any on-screen design stacks up in reality. You can be certain that our understanding of your design problem and the respective theory is safe and sound in the hands of our industry experts.

Despite all the advances in design and simulation software, computers do not tell us all the answers. Reverting back to the textbooks and hand calculations is a regular occurrence and can be lightning quick for working out ballpark estimates and and technical details alike. We also use software like Microsoft Excel for automating calculations, processing many lines of test data and displaying results than can be quickly communicated and readily understood. By choosing Raymont-Osman Product Design, you will also have access to an extensive suite of test and simulation tools to refine the calculations and check them against the performance of real life components
3.14159. or π is one of the most common calculations used within the Design Studio. Check out the below case studies of how Pi has been used to make our products become a reality:
Finding the volume of an oval truncated cone
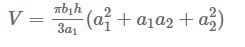
Using the above formula is a typical every-day example of the Maths used by our engineers and designers. Working on a drug-delivery device, we have been able to calculate the volume of an oval come used to measure specific quantities of the drug, whilst preventing it from sticking in the chamber, which would be the case were the design cylindrical. By calculating the volume of the chamber, our team were able to ensure the design was fully calibrated.
Calculating the sheer rates of plastic through an injection mould gate
This is one of the most common applications of Maths within the industry - so much so, that it is used in the production of practically every plastic part. The most common process for manufacturing plastic parts, the injection moulding process involves injecting molten plastic into a mould cavity at very high temperature and pressure, where it then solidifies. Parts are then ejected and the process repeated, with the possibility of over-moulding using a different material (a Twin Shot System) or even over-moulded a second time (Triple Shot System).

Successful injection moulding requires meticulous design to minimise cost, maximise tool life and maintain part functionality. The addition of variables such as extra cores, collapsing cores and material shots has the ability to make the injection moulding process exponentially more complex. The team at Raymont-Osman possess extensive experience of designing the most complex moulding systems, including those involving designing triple shot moulds with several side cores and novel ejection systems.
Working with Speedo to design the Fastskin Pure Focus Goggles, Vue and Virtue Goggles, our Engineers used Pi to calculate the ideal gate size so that the plastic didn't sheer and become damaged during the injection moulding process, whilst still generating sufficient heat for easy flow.


Calculating circumferential speeds
If something moves in a circle motion, then it won’t be long before you need the equations of Circular Motion using Pi. Working on the Equerry Pro Shoe Shiner, Pi was crucial in enabling our team to calculate the speeds of the bristles across the surface of the shoe. In turn, this allowed designers to specify a motor that produced a speed comparable with a hand-held manual brush to ensure a superior shine.

Finding the centre of gravity
The centre of gravity refers to the average location of the weight of an object. Get it wrong, and you have a product which will not stand independently or will easily topple. We can completely describe the motion of any object through space in terms of the translation of the centre of gravity of the object from one place to another, and the rotation of the object about its centre of gravity if it is free to rotate.
Working with the Birmingham 2022 Commonwealth Games provides a perfect example of the importance of understanding the implications of the centre of gravity. An integral aspect of the Baton and the overall package provided by the team at Raymont-Osman was the design and production of a display stand, capable of withstanding the pressures of prolonged international travel, and most importantly of holding the baton upright in a secure position. Using precision diamond-cutters, combined with CNC machining and CAD and CAM software, the design recreates the iconic circular design of the Library of Birmingham as a symbol of the city.

Using Pi to calculate the centre of gravity of the stand, our team were able to determine whether it would actually stand up and how big the base needed to be in order to be certain that the centre of gravity was sufficiently low to ensure stability once the Baton was attached. Through use of Mathematics, this due diligence could be carried out before a single component had even been produced: saving time and money.

To learn more about how we can help you, and bring your product to life, contact us today.
